投稿日: 投稿者: komoriss

偏差値と上位パーセントの対応表

偏差値と上位パーセントの対応表を作成した。受験でよく言われるところの偏差値である。偏差値の数値自体は均等な何かを示しているわけではないので、できるだけ分かりやすい数値に変換してみる。

偏差値を感覚的に理解したい

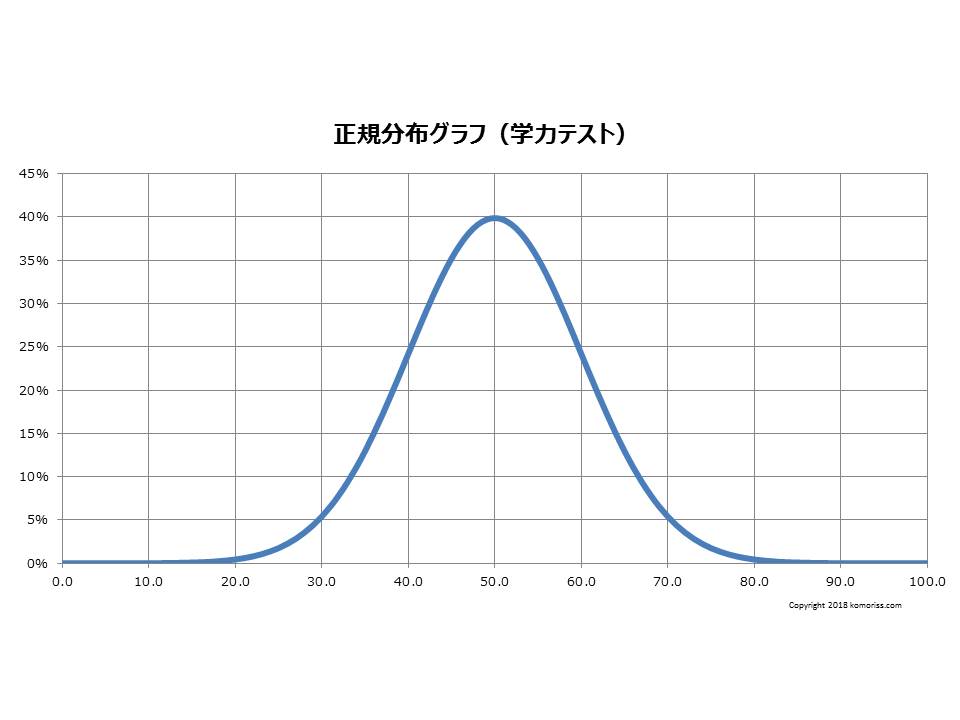
偏差値というのは、母集団が正規分布をする前提で考えるものである。多くの人が集まって色々な特徴を測ってみると、平均値あたりの人が多く、上下に隔たったところで数が減っていくことが多い。このような経験値にも合っていることから、正規分布ということが前提とされている。

偏差値についてはこちらを参照 → 「偏差値とは何か？どのように偏差値が計算されるのか？」

受験や模試等の学力テストでは、平均値を偏差値50になるように、そして平均値+-標準偏差(シグマσ)の位置が偏差値50+-10となるように調整される。これが標準スコアいわゆる偏差値である。これを学力偏差値ともいう。

normal distribution 2

これがわかるようでわかりにくい。もっと感覚的に理解したいと思って、下の表を作った。

偏差値60というのは、平均値から標準偏差(シグマσ)の位置であるので、上位から見ると15.87%となる。また、「何人?」というのは単純にその上位からのパーセントの逆数となる。何か感じるものがあるだろうと思って載せてみた。

偏差値50で「2人」というのは、2人に1人が偏差値50以上と想定されるということだ。要するに偏差値50というのはちょうど真ん中で、自分より下は2人に1人、自分より上も2人に1人という確率であるということだ。

偏差値75ともなると、161人に1人であるということで、161人中1番ということだ。偏差値75というと本当に高い数値だ。例えて言えば、おおよそ40人のクラスが4クラスある学校でほぼ一番であるくらいのイメージである。

実際のテストでは正規分布からは少し外れてこんな感じ（公立高校入試の得点分布）になっている。

実際にはテストはやってみないとわからないので、「案ずるより産むがやすし」という気持ちでまずは何でもやってみよう。

偏差値と上位パーセント・割合の表

偏差値 上位% 何人に一人?
80 0.13% 740.8
79 0.19% 536.0
78 0.26% 391.4
77 0.35% 288.4
76 0.47% 214.5
75 0.62% 161.0
74 0.82% 122.0
73 1.07% 93.2
72 1.39% 71.9
71 1.79% 56.0
70 2.28% 44.0
69 2.87% 34.8
68 3.59% 27.8
67 4.46% 22.4
66 5.48% 18.2
65 6.68% 15.0
64 8.08% 12.4
63 9.68% 10.3
62 11.51% 8.7
61 13.57% 7.4
60 15.87% 6.3
59 18.41% 5.4
58 21.19% 4.7
57 24.20% 4.1
56 27.43% 3.6
55 30.85% 3.2
54 34.46% 2.9
53 38.21% 2.6
52 42.07% 2.4
51 46.02% 2.2
50 50.00% 2.0

科学や産業界では

受験の偏差値では78くらいまでしかない。現実的に意味がないということだろう。ただ、標準偏差σ x 1=偏差値60であり、σ x 2=偏差値70の領域ということになるので、偏差値自体はもっと高い数値も理論的にはありうる。

偏差値 上位% 何人に一人?
85 0.02326291% 4,299
90 0.00316712% 31,574
95 0.00033977% 294,319
100 0.00002867% 3,488,556
105 0.00000190% 52,660,508
110 0.00000010% 1,013,594,635

偏差値110というと10億分の1ということで科学やエンジニアリングの世界で扱うレベルである。偏差値110が+6σにあたるのだが、モノづくりの品質管理で言うシックスシグマというのはこれとは違って、「約3.4ppm」=「約29万分の1」であるという。

品質管理の人がどう計算してそのような数字になったのか詳細は理解できていないが、「ゆらぎ」を考慮したためであるらしい。企業の中で開発や品質管理に関わっている人々にはまた別の厳しい世界があるということである。

上位の全体に占める割合を示すパーセンタイル

偏差値が40の時は、下から15.9%ということになる。偏差値が50の時は全体の真ん中で、これは先ほどと同じ。

偏差値が60になると、偏差値が下位からの分布の積み上げが84.1%になるということを示している。そこそこ良い感じに聞こえるが、相対評価の五段階では5にはちょっと足りないようである。

パーセンタイルは点数ではないが、イメージとしては点数のように感じ取ってもらえると良いかと思う。

偏差値 パーセンタイル
83 100.0
82 99.9
81 99.9
80 99.9
79 99.8
78 99.7
77 99.7
76 99.5
75 99.4
74 99.2
73 98.9
72 98.6
71 98.2
70 97.7
69 97.1
68 96.4
67 95.5
66 94.5
65 93.3
64 91.9
63 90.3
62 88.5
61 86.4
60 84.1
59 81.6
58 78.8
57 75.8
56 72.6
55 69.1
54 65.5
53 61.8
52 57.9
51 54.0
50 50.0
49 46.0
48 42.1
47 38.2
46 34.5
45 30.9
44 27.4
43 24.2
42 21.2
41 18.4
40 15.9
39 13.6
38 11.5
37 9.7
36 8.1
35 6.7
34 5.5
33 4.5
32 3.6
31 2.9
30 2.3
29 1.8
28 1.4
27 1.1
26 0.8
25 0.6
24 0.5
23 0.3
22 0.3
21 0.2
20 0.1
19 0.1
18 0.1
17 0.0

偏差値と順位の対応

偏差値50未満の場合にどうなるのか。上のパーセンタイルでも掴めるのだけれど別の方法で表現する。

また順位で示すとどうなるのか、次の記事で補足説明する。
→「偏差値と順位との対応」

偏差値を上げる方法・「得点できる力」を養う方法

学力偏差値を上げるのは何のためか、どのようにして得点できる力を養う方法については、次の記事を参照してください。
→「偏差値を上げる方法・「得点できる力」を養う方法」

 

関連記事：
・「偏差値と順位との対応」
・「偏差値とは何か？どのように偏差値が計算されるのか？」
・「公立中学校の5段階評価の絶対評価と相対評価、偏差値」
・「都立高校入学試験の得点分布データについて」
・「勉強する目的は、権力に騙されないため、そして自由を勝ち取るため」

“偏差値と上位パーセントの対応表” への9件の返信

  2. 「偏差値と上位パーセント・割合の表」で50%未満も見たいです。

    返信

  3. 偏差値50以下ということだと、例えば
    40 → 84.13%
    30 → 97.72%
    みたいな感じになります

    返信

  4. [偏差値 → パーセンタイルに]
    — 提案 —
    [1] パーセンタイルを追加するのはいかがでしょうか？
    なぜなら、このページを見にくる人が知りたいことだと、私は推察するからです。

    [2] また、並び順は偏差値の低い順の方が分かりやすいような気がします。

    —//—//—
    [変更のBenefit]
    パーセンタイルとは？ (Percentile) // 統計用語
    — Percentile = 能力の得点 = 反対[100人の順位] // 定義の比喩
    //— 例1 —> 競走
    1位 → 100点
    30位 → 70点
    60位 → 40点
    //— 例2 —> 偏差値
    偏差値24 → 0
    偏差値45 → 31
    偏差値47 → 38
    偏差値52 → 58
    偏差値55 → 69
    偏差値65 → 93
    偏差値72~ → 99
    偏差値76~ → 100

    —//—//—
    [求め方] How?
    //— 例1 —> 偏差値55の場合
    偏差値55 > 30.85% > 100-31=69

    //— 例2 —> 偏差値24の場合
    割合の絶対値 [偏差値24 = 偏差値76]
    偏差値76 > 上位0.47% —(四捨五入)—> 0 > 100-0=100

    —//—//—
    この記事は、とても分かりやすく価値が高いので、私はたびたび参考にしています。
    実際に使われる評価が、偏差値からパーセンタイルに変わる一助になれば幸いです。(分かりやすさが大切。日本によくある「あいまいtendency」には口を濁してしまいます…(皮肉でごめんなさい)
    記事を作ってくれてありがとう。愛をこめて。
    Kenji
    natu.soral.123@gmail.com

    返信

  5. 増田 賢治 さん
    コメントありがとうございます。

    確かに低い方からのパーセンタイルがあると分かりやすいように思います。

    パーセンタイルに近いことは https://komoriss.com/standard-score3/ で書いたのですが、1000人中の順位というのが今ひとつなので、そちらを書き直すことにするかもしれません。
    何れにしてもご意見を反映させたいと思います。

    どうもありがとうございます。
    今後ともよろしくお願いします。

    返信

  6. 沖縄の高校1年の孫が全国模試で、偏差値７９だったのですが
    どんなレベルですか？東大京大とか受験出来ますか？
    お忙しいところごめんなさい。

    返信

    1. そのままの成績を保てば偏差値的には充分合格出来るでしょう。ただ、その模試は進研模試という名前ではないでしょうか？進研模試の場合偏差値100も有り得るのであまり参考になりません。増してや、高校1年生の模試となると英数国の三科目でしょうから、日東駒専あたりのレベルの大学を目指して勉強させることをオススメします。

      返信

  7. 1回だけ偏差値-0.03くらいの人を見たことあるんだが、そうとう酷かったんだな…

    返信

  8. 子どものテストの平均点を学期末に集計して、テストの点を目安に、偏差値に当てはめて、なるほど、と納得しています。毎回テストの平均点なんて出しているわけもなく(公立小学校だし)、このサイトで確認して、利用しています。ありがとうございます。偏差値のよき利用方法だと思います！

    返信

コメントを残す

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

このサイトはスパムを低減するために Akismet を使っています。コメントデータの処理方法の詳細はこちらをご覧ください。