偏差値と順位との対応

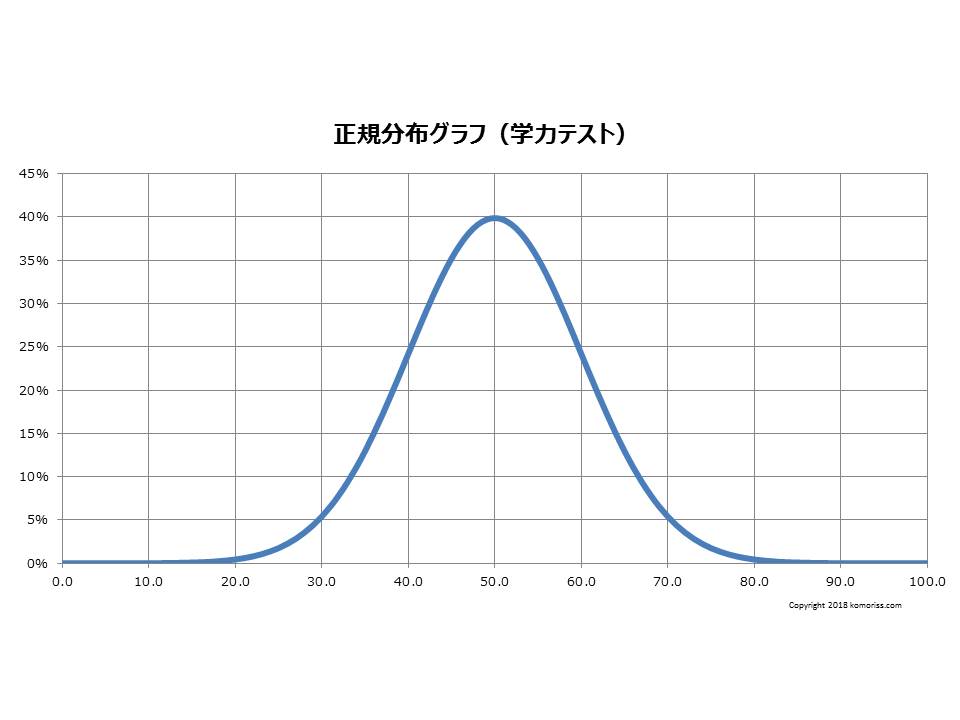
前の記事の「偏差値と上位パーセントの対応表」で、不足している情報があったので補足する。

偏差値と順位との対応

前の記事で、偏差値50以上だけを表記していたのは、上位パーセントを示していたからだ。正規分布は偏差値50を中心とした左右対称だから、偏差値60は上位15.87%であるということは、偏差値40は下位から15.87%ということになる。

正規分布の形は、左右対象である。

偏差値60は、比率で計算すると6.3人に1人ということになり、その反対側の偏差値40では、1.19人に1人ということになる。

1.19人に1人と言っても、これでは全く意味がわからない。1/(1-(1/1.19))と計算すれば約6.3となり、左右対称になっていることが分かる。でもこれはこれでまたピンとこない。

このように同じ意味ではあっても、低い方からのパーセントで言われるのは何だか非常に感じが悪い。

そんなわけで、上位からの順位を示してみた。1000人いる場合の順位を表にしてみた。偏差値80と79の差が出なかったので、小数点以下第一位まで表記した。（学力偏差値について言えば、小数点以下は実質誤差であってあまり意味がないので、気にしなくて良い。）

 

順位（1000人中の順位）

偏差値	順位
80	1.3
79	1.9
78	2.6
77	3.5
76	4.7
75	6.2
74	8.2
73	10.7
72	13.9
71	17.9
70	22.8
69	28.7
68	35.9
67	44.6
66	54.8
65	66.8
64	80.8
63	96.8
62	115.1
61	135.7
60	158.7
59	184.1
58	211.9
57	242.0
56	274.3
55	308.5
54	344.6
53	382.1
52	420.7
51	460.2
50	500.0
49	539.8
48	579.3
47	617.9
46	655.4
45	691.5
44	725.7
42	788.1
41	815.9
40	841.3
39	864.3
38	884.9
37	903.2
36	919.2
35	933.2
34	945.2
33	955.4
32	964.1
31	971.3
30	977.2

偏差値30未満も簡単に計算はできるけれど、学力テストに関して言えば不要であろうと考えて省略した。

前の記事：「偏差値と上位パーセントの対応表」

---

関連記事：
・「公立中学校の5段階評価の絶対評価と相対評価、偏差値」
・「数学用語を英語で言うと・・・？」
・「偏差値とは何か？どのように偏差値が計算されるのか？」

・「勉強する目的は、権力に騙されないため、そして自由を勝ち取るため」