偏差値とは何か? どのような意味があるのか? どのように計算されるのか? 難しい数式を使わずに、わかりやすく説明する。
偏差値とは何か?
偏差値とは、テストの点数や身長・体重などの数値が、集団の中で平均値を中心にして、上や下へどれだけ隔たりがあるかを表す指標である。
一般的に、このようなばらつきのあるものは正規分布すると考えられている。学力テストにおいても正規分布に近似するという前提で、偏差値が計算されている。
さらに受験で用いられる偏差値では、平均値が偏差値=50となるように調整されており、ばらつきは標準化されている。
以降は、学力テストで用いられる偏差値について書く。
関連記事も参照:
・「偏差値と上位パーセントの対応表」
・「偏差値と順位との対応」
学力テストの偏差値とは
偏差値50は、平均値の位置にあり、順位としては全体の真ん中であることを意味する。ばらつきを表す標準偏差(シグマあるいはσ)が10となるように調整されている。
試験を受けた全員の得点を計算して、標準偏差が得られる。
標準偏差の求め方
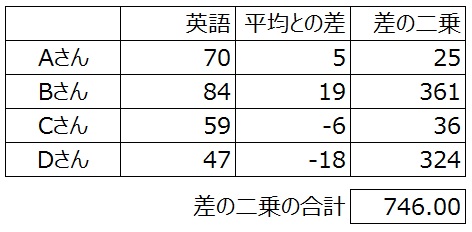
受験者一人ずつの得点と平均点との差を二乗した数値を、全員分合計して、それを人数で割り、その平方根が標準偏差である。
この例では、4人が実施したテストから標準偏差を求める。まず平均点を計算する。次に一人ずつ平均との差を計算して、それを二乗する。その数値を全員分足す。これが平均との差の二乗の合計である。746という計算になった。
この数字を人数4で割ると186.5となり、その平方根を計算すると、約13.66となる。これがこの英語のテストの標準偏差である。
標準偏差は、その得点のばらつきを表すもので、標準偏差が大きければ平均を中心としたばらつきが大きく、標準偏差が小さければばらつきが少ないということになる。
得点を全員分計算する必要があるので、受験者がテストの平均点と自分の得点だけしか知らされない場合には、標準偏差を知ることはできない。したがって、自分の偏差値を計算することはできない。
個々の偏差値の求め方
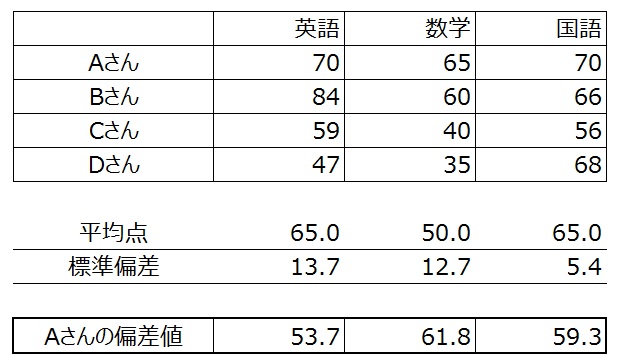
個々の受験者の偏差値は、次のように求められる。
( 得点 一 平均点 )÷ 標準偏差 × 10 + 50
個々の偏差値では、全体のテストのばらつきが考慮される。英語と国語はどちらも平均点が65点で、Aさんはどちらも70点を取っているが、国語の方が偏差値が高くなっている。英語と国語のばらつきが異なるからだ。
数学の得点は、英語や国語よりも低いけれど、平均点も低く3教科の中ではAさんとしては一番高い偏差値になっている。
TOEICのような資格認定テストでは、受験者の得点や分布、試験の標準偏差などが公開されているものもある。しかし、入試では、標準偏差は公開されないことが一般的だ。だから、模試などの得点から学力を測る必要がある。
正規分布について
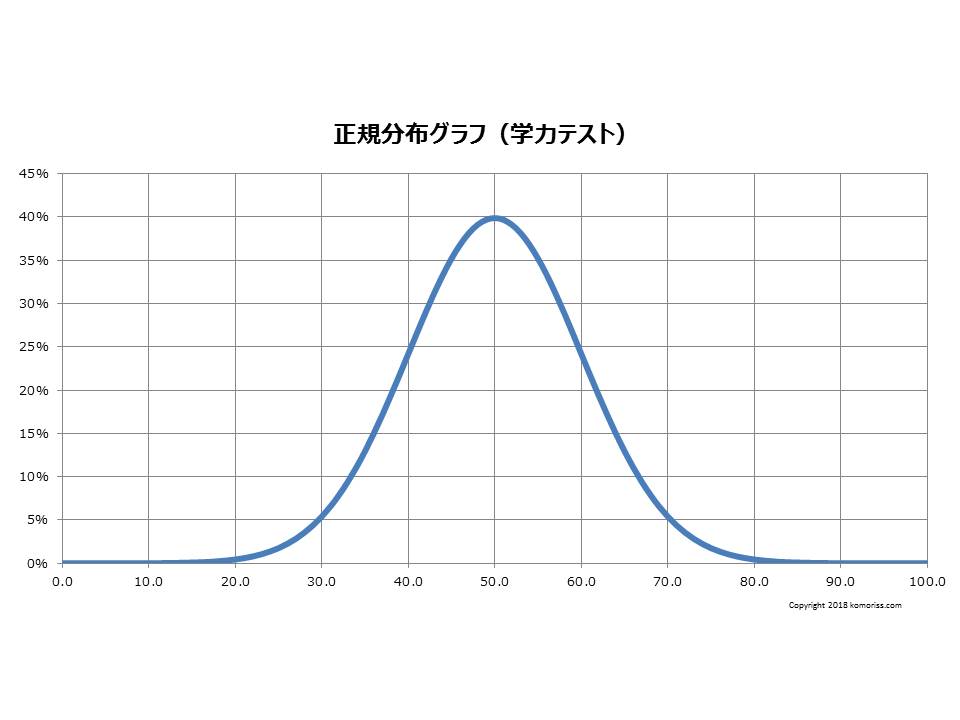
次に、正規分布のグラフを示す。理想的な標本の分布を前提としているので、左右に均等に綺麗な形になっている。
このグラフでは、平均点を取る受験者が一番多く、左右に同じように広がっている。両極端もどんどんと少なくはなるがゼロにはならない。(実際のテストでは受験者が一定の数なので、両端には限りがある)
このグラフは正規分布グラフというもので、テスト結果がこのような分布をしていると仮定して計算される。
この図の横軸の40.0から60.0の間に入る確率は、68.27%である(これは平均点から上下に1標準偏差内(±σ)という意味である)。また、30.0から70.0の間に入る確率は、95.45%となる。20.0から80.0の間に入る確率は、99.73%である。
偏差値が60.0以上になる確率は何パーセントか、と考えるときには、この数字を用いて、100 – 68.27 = 31.73 で、上位だけを見るので2で割るとおよそ15.87%となる。
同様に、偏差値70.0であれば、100-95.45=4.55で、2で割ると2.28%となる。偏差値80.0の時は、0.13%となる。
これをわかりやすい表にしたものがこのページである。
→「偏差値と上位パーセントの対応表」
十分に受験者数が多くて、試験問題が学力のレベルを幅広く測れるようになっており、受験者も極端な偏りがない場合には、このようなグラフの形となるのだろう。
関連記事:
・「偏差値と上位パーセントの対応表」
・「偏差値と順位との対応」
・「公立中学校の5段階評価の絶対評価と相対評価、偏差値」
・「都立高校入学試験の得点分布データについて」