ヨーロッパでは古くから様々な調律方法が考案されてきた。古い時代の調律ではすべての調を弾くことはできなかった。それから、新しい調律方法が開発されて、全ての調を弾くことが可能になった。
J.S.バッハの時代に、すべての調を弾くことができようになり、有名な「平均律曲集」が作曲された。でも、これは現代の平均律とは違うものだ。バッハの時代の平均律は、今では古典調律という。20世紀に入ってから普及した、現代の平均律以前の調律を古典調律と言う。
古典調律には、さまざまな種類がある。バッハの時代の平均律は、ちょっと聞くだけでは現代の平均律に近い。しかし、調が変わると和音や旋律の雰囲気が変わるため、作曲者も曲想に合わせた調を選んでいたのだ。
平均律とは何か?
まずは基本的な事柄をQ&Aの形で進める。
Q:平均律とは何か?
A:現代では12音を機械的に均等にした音程でチューニングすること。バッハの時代から20世紀初頭にかけて「平均律」という言葉は、綺麗に調律された状態を表す言葉だったので、実際には様々な調律方法があった。
Q:バッハの平均律というのは、現代の平均律と同じ?
A:同じではない。ドイツ語や英語の平均律というのは、「良く調律された」という意味の言葉で、たくさんの調が弾けるという意味で使われた。ドイツ語では、Wohltemperierteといい、英語では well tempered という。
Q:バッハの平均律と現代の平均律を区別する呼び方は?
A:どちらも「平均律」と呼ばれることがある。区別する場合には、現代の12音が均等な調律を「12平均律」という。12平均律が20世紀に普及するまでは、別の不均等な「平均律」があったのだが、こちらは「古典調律」と呼ばれる。さらに「ヴェルクマイスター第1技法3番」など個別の調律方法を付けることが多い。近年では、音律の知識が普及してきたので、バッハの時代の音律を「平均律」と呼ぶことはなくなった。
Q:現代の均等な12音のチューニングはいつ頃できたのか?
A:理論的にはすでに19世紀以前には考案されてはいたが、ピアノで実際に調律がされるようになったのは、20世紀に入ってからと考えられている。バッハはもちろん、モーツァルトもベートーヴェンもショパンもドビュッシーも現代の機械的12音均等の調律は経験したことがなかった。
Q:オクターヴ上の音は、周波数がどれだけ高くなるのか?
A:オクターヴ高くなると周波数は倍になる。人間が感じる音程というのは周波数の比率である。倍だとオクターブ、1.5倍だと完全5度、という音程に感じられる。
Q:12平均律では半音の周波数比率は?
A:$$2^{\frac{1}{12}} = 1.059463094359\ldots$$
Q:12平均律では完全5度の周波数比率は?
A:$$2^{\frac{7}{12}} = 1.498307076877\ldots$$
純正な完全5度は1.5なので、それよりも少し狭い。
Q:セント値というのは?
A:オクターブを周波数比で1200に均等に分割した単位のこと。12平均律では、それぞれの半音の差が100セントになる。1セントの周波数比は、
$$2^{\frac{1}{1200}} = 1.000577789507\ldots$$
nセントの時の周波数の比は、$$2^{\frac{n}{1200}}$$である。
Q:周波数比が1.5の時のセント値の求め方は?
A:セント値をc、周波数比をrとすると、
$$c=1200 \cdot \log_{2} r$$
なので、表計算ソフトでは =1200*log(1.5,2) とすると、701.9550009…と計算される。約702セントである。
古典調律とは何か?
Q:古典調律とは何か?
A:20世紀に普及した12音が機械的に均等な調律(12平均律)が登場する以前の調律を総称して古典調律という。
Q:どのような種類があるのか?
A:数十種類の調律方法が伝えられている。それらの古典調律は、現代では価値が再確認されて多く演奏されるようになった。
ピタゴラス音律、純正律、中全音律(ミーントーン)、ヴェルクマイスター、キルンベルガーなどが有名である。
Q:ヴァイオリンなど演奏者が音程を作る楽器ではどんな音程?
A:弦楽器や管楽器、声楽などでメロディーを弾く(歌う)時には、ピタゴラス音律に近い音程で演奏する。一方、金管アンサンブルとか合唱などで和音を綺麗に響かせるために、ピタゴラス音律では3度や6度がうなりが気になるので、純正律に近づけて演奏する。
オルガンやチェンバロは、演奏中に音程が変えられないので、このピタゴラス音律と純正律の協和感を両立することができない。そこで、これらを融合させて新しい調律方法を作ろうと、試行錯誤を続けてきた。
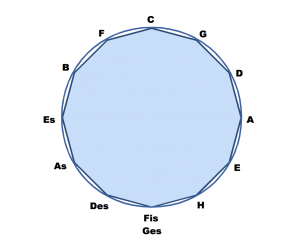
全ての調律の問題は解決されない5度圏図にある
ある音のピッチを決めてから、その他の音程を決めていく。
最初にCを決めて、1.5倍の周波数にGを合わせると、「うなり」がなく完全に協和する音程になる。
次にGの1.5倍の音程を取る。Dである。ずっと音を上げていくと高くなりすぎるので、だいぶ上がったら1/2の周波数に、つまりオクターブ下げる。
Gから3/4の周波数にすると完全4度下のD音が取れる。これも「うなり」無しの完全協和音である。
こうして、完全5度上げて、完全4度下げていく。
C→G→D→A→E→H→Fis→Des→As→Es→B→F→(C)
そして、Fの次にCが綺麗に決まって、つまり元のCの音程になるかと期待すると、そうはいかず音はかなり外れてしまうのだ。
5度ずつ上がっていき、CからCまで12ステップで戻ってくると、
$$\left( \frac{ 3 }{ 2 } \right )^{12}$$
ということになる。これは元の音の7オクターブ上になってしまうので、これを7オクターブ下げねばならない。1/2を7乗する。
$$\left( \frac{ 1 }{ 2 } \right )^{7}$$
つまり、元の音に戻そうとすると、
$$\left( \frac{ 3 }{ 2 } \right )^{12} \cdot \left( \frac{ 1 }{ 2 } \right )^{7}$$
$$=\frac{3^{12}}{2^{19}}$$
となり、これを計算すると、約1.01364326477となる。
この周波数の差を音程に換算すると23.460セントになる。100セントが半音なので、かなりのズレだ。約4分の1半音もある。
(これをピタゴラス・コンマという)
このズレを5度圏の中で割り振りながら、配分することが中世からの課題であり大変な苦労があった。20世紀以降は機械的に処理されることになる。しかし、19世紀以前には、音は大切にされていて、5度圏のズレを解決しようとする方法には、アイディアや美的センスが最大限に活かされていた。
とても奥が深い古典調律
バッハがその調律方法に感動して、平均律曲集を作ったと言われるのは、ヴェルクマイスターの調律方法がとても綺麗だったからだと思われる。この調律方法の特徴は、C-Dur、F-Durでは、和音が純正律の響きになる。そして、Des-Durのスケールを弾くとピタゴラス音律になる。
ざっくり言えば、シャープ、フラットが少ないと、純正律のような響きになり、シャープ・フラットが増えた時は、ヴァイオリンが奏でるようなピタゴラス音律としてメロディーとして弾くことができる。
つまり、調性はただ単にピッチが変わるだけではなくて、音階を構成する音律が変化するので、曲の音階が変わる。その結果、調性が変わると、曲の雰囲気ががらっと変わることになる。調性が音楽とともに生きていたのだ。
このことは、モーツァルト、べートーヴェンの作品についてはもちろんの事、ショパン、ドビュッシーの曲においても、調性の影響が音楽の構成に緊密に繋がっている。
移調した時に、12平均律ではただ単にピッチの平行移動に過ぎないのだけれども、古典調律の時代には調によって音程関係が変わって曲の雰囲気が変わっていく。
各調の音階を(移動ド唱法的に)ドレミファソラシドと弾くと、12種類の音階が得られる。12平均律では1種類しかないのに、12種類の音階が鳴る。ごく微妙な音程のずれは、違和感としてではなくて調性の個性として生きている。
古典調律の種類
主な古典調律について、それらが成り立ってきた順を追って説明することにする。
ピタゴラス音律(Pythagorean tuning)
ピタゴラス音律は、純正な完全5度をベースにして作られた音階の音程を定めたものである。純正な完全5度は、周波数比が正確に3:2で、これとオクターブの2:1を組み合わせて、音程を取っていく。
中世の教会音楽はピタゴラス音律である。また、現代でも声楽やヴァイオリオンのメロディーはピタゴラス音律が多く使われている。
つまりは、自然なメロディーで、正確に音程が合っているように感じられるのは、ピタゴラス音律である。ピタゴラスが研究したことでこの名前がある。
ピタゴラス音律は次のように導かれる。(ドイツ音名で表記)
・Cをベースにすると、5度上のGを3/2のピッチにする
・Gから4度下のDを 3/2・1/2 =3/4のピッチにする
・Dから5度上のAを3/2のピッチにする
・Aから4度下のEを3/4のピッチにする
・Eから5度上のHを3/2のピッチにする
・忘れていたFをCの4度上の4/3のピッチにする
(オクターブ上のCから5度下なので、2割る3/2 = 2・2/3 = 4/3)
この順番に沿って、ピタゴラス音律を分数で計算する。
C = 1
G = 3/2
D = 3/2・3/4 = 9/8
A = 9/8・3/2 = 27/16
E = 27/16・3/4 = 81/64
H = 81/64・3/2 = 243/128
F = 4/3
これを音名の順番にする。最後にオクターブ上のCを付けると、ドレミファソラシドの音階ができる。
C = 1
D = 9/8
E = 81/64
F = 4/3
G = 3/2
A = 27/16
H = 243/128
C = 2
これがピタゴラス音律である。この分数の世界が半音の世界に進んでいっても、矛盾なく成り立つであろうと西欧世界では期待したけれど、実際には5度圏は閉じることはできなかった。
この分数をセント値に計算してみる。
| 音名 | 周波数比 | セント値 | 差(セント値) |
| C=1 | 1.0000 | 0.000 | – |
| D=9/8 | 1.1250 | 203.910 | 203.910 |
| E=81/64 | 1.2656 | 407.820 | 203.910 |
| F=4/3 | 1.3333 | 498.045 | 90.225 |
| G=3/2 | 1.5000 | 701.955 | 203.910 |
| A=27/16 | 1.6875 | 905.865 | 203.910 |
| H=243/128 | 1.8984 | 1109.775 | 203.910 |
| C=2 | 2.0000 | 1200.000 | 90.225 |
音程の差を見てみると、12平均律よりも全音が少し広く、半音が狭いことが分かる。
| 音階 | 音程の差 |
| C=1 | |
| | | 203.910 |
| D=9/8 | |
| | | 203.910 |
| E=81/64 | |
| | | 90.225 |
| F=4/3 | |
| | | 203.910 |
| G=3/2 | |
| | | 203.910 |
| A=27/16 | |
| | | 203.910 |
| H=243/128 | |
| | | 90.225 |
| C=2 |
純正律(Just Intonation)
ピタゴラス音律の単旋律はとても気持ちが良い。しかし、和音を入れようとすると中世の教会では「うなり」が嫌われていたので、オクターブと完全5度と完全4度だけしか使えなかった。
そこで和音を綺麗にならすための、工夫がされた。それが純正律である。
ピタゴラス音律では、完全8度(オクターブ)、完全5度、完全4度が使えるが、これに3度と6度も協和させたい。
そこでC-Eを純正の長3度に、C-Aを純正の長6度にするべく、E=5/4、A=5/3とする。分数が単純であるほど音はうなりが少ない。
GとHの間の3度も元のままでは不協和なので、Gの3/2にC-E間の音程5/4をかけて、3/2・5/4=15/8とした。
| 音名 | 周波数比 | セント値 | 差(セント値) |
| C=1 | 1.0000 | 0.000 | – |
| D=9/8 | 1.1250 | 203.910 | 203.910 |
| E=5/4 | 1.2500 | 386.314 | 182.404 |
| F=4/3 | 1.3333 | 498.045 | 111.731 |
| G=3/2 | 1.5000 | 701.955 | 203.910 |
| A=5/3 | 1.6667 | 884.359 | 182.404 |
| H=15/8 | 1.8750 | 1088.269 | 203.910 |
| C=2 | 2.0000 | 1200.000 | 111.731 |
全音は2種類になっている。C-D、F-G、A-Hの音程は広いので大全音という。これに対して、D-E、G-Aの音程は狭いので小全音という。
2種類の全音があるため、音階が不均等になるのは欠点である。
3度と6度が大幅に改善されたが、5度の組み合わせを見てみるとD-Aの5度は不協和となる。周波数比は40:27。
H-Fの5度は減5度で元々協和しない。周波数比は64:45。
| 5度 | 低音 | 高音 | 比 | セント値 |
| C-G | 1.0000 | 1.5000 | 1.5000 | 701.955 |
| D-A | 1.1250 | 1.6667 | 1.4815 | 680.449 |
| E-H | 1.2500 | 1.8750 | 1.5000 | 701.955 |
| F-C | 1.3333 | 2.0000 | 1.5000 | 701.955 |
| G-D | 1.5000 | 2.2500 | 1.5000 | 701.955 |
| A-E | 1.6667 | 2.5000 | 1.5000 | 701.955 |
| H-F | 1.8750 | 2.6667 | 1.4222 | 609.776 |
3度を見てみる。
| 3度 | 低音 | 高音 | 比 | セント値 |
| C-E | 1.0000 | 1.2500 | 1.2500 | 386.314 |
| D-F | 1.1250 | 1.3333 | 1.1852 | 294.135 |
| E-G | 1.2500 | 1.5000 | 1.2000 | 315.641 |
| F-A | 1.3333 | 1.6667 | 1.2500 | 386.314 |
| G-H | 1.5000 | 1.8750 | 1.2500 | 386.314 |
| A-C | 1.6667 | 2.0000 | 1.2000 | 315.641 |
| H-D | 1.8750 | 2.2500 | 1.2000 | 315.641 |
3度はC-E、F-A、G-Hの3種類は、長3度で音程が広い。そして、完全5度や完全4度に次いで、協和する。周波数比は5:4。
E-G、A-C、H-Dの3種類は、短3度で長3度よりも約半音だけ音程が狭い。長3度より協和の程度は少ないがそれでも十分に協和音とみなされた。周波数比は6:5。
最後の一つ、D-Fの3度は不協和音として残ってしまう。周波数比は32:27。
次は6度について見てみる。
| 6度 | 低音 | 高音 | 比 | セント値 |
| C-A | 1.0000 | 1.6667 | 1.6667 | 884.359 |
| D-H | 1.1250 | 1.8750 | 1.6667 | 884.359 |
| E-C | 1.2500 | 2.0000 | 1.6000 | 813.686 |
| F-D | 1.3333 | 2.2500 | 1.6875 | 905.865 |
| G-E | 1.5000 | 2.5000 | 1.6667 | 884.359 |
| A-F | 1.6667 | 2.6667 | 1.6000 | 813.686 |
| H-G | 1.8750 | 3.0000 | 1.6000 | 813.686 |
C-A、D-H、G-Eが長6度で協和する。周波数比は5:3。
E-C、A-F、H-Gが短6度で協和する。周波数比は8:5。
残るF-Dが、不協和となる。周波数比は27:16。
このように純正律では、ピタゴラス音律と比べると、D-Aの5度は逆に不協和になったが、純正律の3度と6度が使えるようになった効果は大きかった。
D-Fの3度、F-Dの6度は不協和であるけれども、これらの音程を避けるなどの工夫をすれば良い。
中全音律(Meantone temperament)
ミーントーンともいう。中全音律の狙いは、純正律の不均等な音階を是正して、なおかつ3度や6度の協和を保つことである。
純正律の大全音と小全音がその中間の音程になったので、中全音律という。
中世のピタゴラス音律の3度は不協和音とされてきたが、時代はルネサンスに入ると3度の音程も多く使われるようになった。
中全音律には種類があり、1/4コンマ中全音律、1/3コンマ中全音律などがあるが、1/4コンマ中全音律が最も一般的だ。以降は、1/4コンマ中全音律について説明する。
音程が狭くて不協和だった純正律のD-Aを広げて、その他の純正5度を少し狭めている。
中全音律は次のようにして導くことができる
Cを基準にする。(ドイツ音名で表記)
・Cから上にEを純正な長3度のピッチにする
(この後、Dを作るためにC-Eの上下に仮のピッチを作る)
・Eの5度上に、純正5度でHを作る(仮)
・Hの4度下に、純正4度でFisを作る(仮)
・Cの5度下に、純正5度でFを作る(仮)
・Fの4度上に、純正4度でBを作る(仮)
・BとFisのちょうど中間のピッチを作ってDとする
(実際には、仮のBの上の純正3度より11セント高くDを作る)
・オクターヴ上げたCとこのDの間に、中間のピッチにGを作る
(Cの上の純正4度よりほんのわずか5セント高いところにG)
・同じように、DとEのちょうど中間となるピッチでAを作る
・Aから上にCisを純正長3度に合わせる
・Aから下にFを純正長3度に合わせる
・Gから上にHを純正長3度に合わせる
・Gから下にEsを純正長3度に合わせる
・Dから上にFisを純正長3度に合わせる
・Dから下にBを純正長3度に合わせる
・Eから上にGisを純正長3度に合わせる
純正律よりも進化しており、半音階が全て定まった。
| 音名 | セント値 |
| C | 0.000 |
| Cis | 76.049 |
| D | 193.157 |
| Es | 310.265 |
| E | 386.314 |
| F | 503.422 |
| Fis | 579.471 |
| G | 696.578 |
| Gis | 772.627 |
| A | 889.735 |
| B | 1006.843 |
| H | 1082.892 |
| C | 1200.000 |
純正の長3度は8つあり、残りの4つは音程が広く不協和になる。Cis-F、Fis-B、Gis-A、H-Esの4つ。
| 長3度 | セント値 |
| C-E | 386.314 |
| Cis-F | 427.373 |
| D-Fis | 386.314 |
| Es-G | 386.314 |
| E-Gis | 386.314 |
| F-A | 386.314 |
| Fis-B | 427.373 |
| G-H | 386.314 |
| Gis-C | 427.373 |
| A-Cis | 386.314 |
| B-D | 386.314 |
| H-Es | 427.373 |
| C-E | 386.314 |
完全5度は、均等によく調整されているが、Gis-Esの間が極端に広くなっている。
| 完全5度 | セント値 |
| C-G | 696.578 |
| Cis-Gis | 696.578 |
| D-A | 696.578 |
| Es-B | 696.578 |
| E-H | 696.578 |
| F-C | 696.578 |
| Fis-Cis | 696.578 |
| G-D | 696.578 |
| Gis-Es | 737.637 |
| A-E | 696.578 |
| B-F | 696.578 |
| H-Fis | 696.578 |
| C-G | 696.578 |
こうして中全音律では、多くの調が弾けるようになった。中全音律は、15世紀にヨーロッパで普及し始めて、19世紀頃まで鍵盤楽器の調律で使われている。
ヴェルクマイスター音律
ヴェルクマイスター音律は、アンドレス・ヴェルクマイスターが自身の著作に記した調律方法である。1691年の論文でその方法が示された。
ヴェルクマイスターは、4つの方法を示した。第1技法第3番、第2技法第4番、第3技法第5番、第4技法第6番である。
第x技法というのは、論文内の順番を示すもので、後ろの第3番というのはモノコード(1本の弦で音程を測る器具)の番号である。
2種類の独立した番号を併記しているだけで、第1技法に3種類あるわけではなく、「第1技法=第3番」であり、第1技法は一つだけである。
ちなみに、モノコードの1番には純正律が、2番には中全音律(ミーントーン)が充てられている。
ヴェルクマイスター第1技法第3番
これが最も一般的で普及しており、ヴェルクマイスターと言えば、まずこの音律のことを指している。
ヴェルクマイスターは、「1/4コンマ分割に基づく正しい調律」とした。
ヴェルクマイスター音律にチューニングする方法は実は結構難しい。インターネットや書籍にも正確な調律方法は載っていない。
理論値であるので、「うなり」などを聞きながら、細心の注意で合わせていくことが求められている。しかし、もっと簡易な方法があるはずだ。
Cを基準音として、Cから下に純正5度を合わせていくところは容易にできる。
(ドイツ音名)
・Cから下にFを純正の5度に合わせる
・FからBを純正の5度に合わせる
・BからEsを純正の5度に合わせる
・EsからAsを純正の5度に合わせる
・AsからDesを純正の5度に合わせる
| 音名 | ヴェルクマイスター | 計算式 |
| C | 0.000 | =1 |
| Cis | 90.225 | =256/243 |
| D | 192.180 | =64/81*2^(1/2) |
| Es | 294.135 | =32/27 |
| E | 390.225 | =256/243*2^(1/4) |
| F | 498.045 | =4/3 |
| Fis | 588.270 | =1024/729 |
| G | 696.090 | =8/9*8^(1/4) |
| Gis | 792.180 | =8/9*8^(1/4) |
| A | 888.270 | =1024/729*2^(1/4) |
| B | 996.090 | =16/9 |
| H | 1092.180 | =128/81*2^(1/4) |
| C | 1200.000 | =2 |
中全音律のDの音は、193.157セントであるが、ヴェルクマイスターのD音は192.180であるが、1セントだけ下げるというようなことは実用的には無理である。
| 音名 | ヴェルクマイスター | 中全音律 | 差(絶対値) |
| C | 0.000 | 0.000 | 0.000 |
| Cis | 90.225 | 76.049 | 14.176 |
| D | 192.180 | 193.157 | 0.977 |
| Es | 294.135 | 310.265 | 16.130 |
| E | 390.225 | 386.314 | 3.911 |
| F | 498.045 | 503.422 | 5.377 |
| Fis | 588.270 | 579.471 | 8.799 |
| G | 696.090 | 696.578 | 0.488 |
| Gis | 792.180 | 772.627 | 19.553 |
| A | 888.270 | 889.735 | 1.465 |
| B | 996.090 | 1006.843 | 10.753 |
| H | 1092.180 | 1082.892 | 9.288 |
| C | 1200.000 | 1200.000 | 0.000 |
中全音律のGとは音程が近い。うまく調律するためのヒントは、このあたりにありそうだ。
ピタゴラスコンマの約24セントを4つの五度に振り分けた結果、このようになる。
まあ、とにもかくにも、ヴェルクマイスターの音律によって、12の長短の各調が演奏できるようになった。
ヴェルクマイスター第3技法第5番
この音律は、12平均律に大変近くなっている。この調律は滅多に聞くことがない。中途半端な12平均律に聞こえてしまうかもしれない。
| 音名 | セント値 |
| C | 0.000 |
| Cis | 96.090 |
| D | 203.910 |
| Es | 300.000 |
| E | 396.090 |
| F | 503.910 |
| Fis | 600.000 |
| G | 701.955 |
| Gis | 792.180 |
| A | 900.000 |
| B | 1001.955 |
| H | 1098.045 |
| C | 1200.000 |
古典調律とピッチの関係
ピッチについては、以前に「なぜバロック調律は415Hzになったのか?」に詳しく書いているので、こちらを参照していただきたい。
実はそれだけではなくて、音律と関係したピッチについての話がある。現代ではA音を基準に調律をすることが多い。
バロックの頃には、チェンバロの音を基準にして、バイオリンも各音を合わせることも行われたようである。
現代のオーケストラで、オーボエが基準ピッチを鳴らして、他の楽器がそれに合わせるのは、オーボエには管を抜いたり深く差したりして合わせるジョイントがなくて調節ができないからだ。ファゴットは事前にオーボエと合わせておく必要もある。
バロックのピッチは、今よりも低かったが、どのようなピッチで合わせたかは、なぜバロック調律は415Hzになったのか?に書いたように様々であったようだ。
現代でA音を基準にして、ピッチを440Hzや442Hzとしながらも、ヴェルクマイスターのような調律をするケースもないわけではない。
A音を基準にした場合には、下の表のように、C音、F音、G音がかなり高くなる。A=440Hzとした場合の、音高がC4からC5の場合のズレを表にした。
・音名:ドイツ音名(表は低い方のC4からオクターブ上のC5まで)
・セント値:ヴェルクマイスターでCをゼロとした音高
・Aとの差(セント値):Aをゼロとして、12平均律の音高との差
・ピッチ差(Hz);A基準で12平均律の音高との周波数の差(Hz)
| 音名 | セント値 | Aとの差(セント値) | ピッチ差(Hz) |
| C | 0.000 | 11.730 | 1.7787 |
| Cis | 90.225 | 1.955 | 0.3132 |
| D | 192.180 | 3.910 | 0.6640 |
| Es | 294.135 | 5.865 | 1.0558 |
| E | 390.225 | 1.955 | 0.3724 |
| F | 498.045 | 9.775 | 1.9774 |
| Fis | 588.270 | 0.000 | 0.0000 |
| G | 696.090 | 7.820 | 1.7747 |
| Gis | 792.180 | 3.910 | 0.9390 |
| A | 888.270 | 0.000 | 0.0000 |
| B | 996.090 | 7.820 | 2.1104 |
| H | 1092.180 | 3.910 | 1.1167 |
| C | 1200.000 | 11.730 | 3.5573 |
Aを基準として、ピッチを440Hzや442Hzとすると他の音が全て高くなってしまい、通常の調律のピアノでこれだけ音高を全体であげるとなると、調律はすぐには安定しない。
音高の上げ下げが大きくなるという理由で、ほとんど全ての公共のホールでは備え付けのピアノを12平均律以外に調律することが禁止されているようだ。
ホールとしては古典調律ならチェンバロでやってくれということなのだが、ヴェルクマイスターの調律方法は、もともとはチェンバロのために考案されたものであるが、ピアノの時代に変わっても、20世紀初頭まで多くのピアノで調律されていた。
バッハ、モーツァルトはもちろん(彼は中全音律だったらしい)、ハイドン、シューベルト、ベートーヴェン、リスト、ショパン、シューマン、ブラームス、メンデルスゾーン、チャイコフスキー、ワーグナー、ドヴォルザーク、ドビュッシー、これら全ての作曲家の時代のピアノは、12平均律ではなくて古典調律だったのである。
ということは、今の時代に普通に聞いているクラシック音楽の中でもピアノ音楽は、現代の音律に変更したものだということになる。ピアノ音楽では現代の調律の方が響きに緊張感があって良いという人もいる。
実は、世界で最初のピアノが発明されてから現代に至るまで歴史的には古典調律でチューニングされていた期間の方が長い。
現代のピアノを古典調律にすることは、一般的にはあまり好まれないようだが、平島達司著『増補ゼロ・ビートの再発見』(東京音楽社)ではドビュッシーやショパンの曲を古典調律で演奏した方が、調性のカラーがくっきりして、作曲者の意図も明確に聞こえてはるかに美しいと言う。
関連コンテンツ:
・「なぜバロック調律は415Hzになったのか?」
・「世界で最初のピアノ」
・「オルガンの調律」