地上の2地点の距離を緯度と経度から計算する。地球は真球ではなく回転楕円体に近いので、より高い精度を求めるならば回転楕円体による計算をする必要がある。しかし地球を真球をとして計算しても実用的には十分な数値が得られる。ヒュベニの近似式による計算方法も追加した。
緯度経度から2地点の距離を計算
真球として計算するので、長半径と短半径のどれを使うのかというと、平均半径を使用する。平均半径にも色々な考え方があり、いろいろな数値がある。最初はGoogle Mapで使用されている方法で計算する。真球として計算され、地球の半径を6371kmとしている。
球面上の最短距離(D)を求める公式を下に示す。地中を貫通する最短距離ではなく、表面に沿った距離だ。単位はkmである。2地点の座標は地点1が(緯度=lat1, 経度=lon1)、地点2(緯度=lat2, 経度=lon2)とする。
$$D = 6371・arccos(cos(lat1)*cos(lat2)\\*cos(lon2-lon1)\\+sin(lat1)*sin(lat2))$$
ここで緯度と経度はラジアンでの表記が求められる。度数をラジアンに換算するには、πを掛けて180で割れば良い。
エクセルなど表計算ソフトで計算する
表計算ソフトに次のように緯度と経度を入力する。
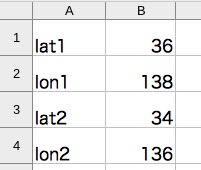
別のセルには次のように入力する。
=6371 * ACOS(COS(B1*PI()/180) * COS(B3*PI()/180) * COS(B4*PI()/180-B2*PI()/180) + SIN(B1*PI()/180) * SIN(B3*PI()/180) )
すると、上記の二つの緯度と経度から距離を計算する。
287.461514159 のように表示されることが多いだろう(アプリの桁数表示に寄って異なるはず)。単位はkmなので、おおよそ287.4kmと計算できる。国土地理院サイトでは287,325.451(m)である。
また北緯と南緯、東経と西経があるので、ここでは北緯はプラスの数値で、南緯はマイナスの数値とし、同様に東経をプラスで西経をマイナス数値にすれば、この式で計算できる。
度数は、度分秒ではなく十進の数値で入れる。北緯であれば35.9876のように設定する。
回転楕円体としての距離計算
回転楕円体として距離を計算するのは実は大変に難しいことが分かった。簡単に計算できる公式が見つからない。
国土地理院のサイトでは、かなり正確と思われる距離の計算を得ることができる。しかし、それでも実測ではないので、あくまでも理論値ということになる。GRS80(<-besselも選択できる)という地球に近似した楕円体モデルの上での計算になる。
地球は、地殻やマントルも均一ではないし、地下の重金属の分布によっても重力の不均衡がある。現実の平面は実測しないと分からないが、ある程度の誤差を受け入れることで、計算が容易になるということだ。
国土地理院の式は繰り返しの計算指示などがあり複雑でシステム化しにくいので、たとえ精度はもっと劣っていてももっと簡単で扱いやすい計算式がないかと探す。
ポーランド系アメリカ人のThaddeus Vincentyが開発した数式もVincenty法として使われており精度も高いようだが、Vincenty法にも反復計算が含まれるので表計算ソフトでは簡単に計算できない。
そこで、K.ヒュベニ(Karl Hubeny)が1950年代に考案した平均緯度式の測地線長を算出方法というのを試してみる。
ヒュベニの近似式
日本では、カシミール3Dで使用されたことで話題になり、K.Hubenyの簡略式がこの業界では有名になった。
$$d=\sqrt { (M・\Delta φ)^2 + (N・cos φ・\Delta λ)^2 }$$
d:2点間の距離(単位はメートル)
φ:2点の平均緯度
Δφ:2点の緯度差
Δλ:2点の経度差
a:回転楕円体の長半径 ※注
M:子午線曲率半径
N:卯酉線曲率半径
e:離心率
$$M = \frac{a(1-e^2)}{ \sqrt {((1-e^2*sinφ^2)^3)} } $$
$$N = \frac{a} {\sqrt{ (1-e^2*sinφ^2)} } $$
$$e = \sqrt{1 – \frac {{b}^2} {{a}^2} } $$
※注 a: 回転楕円体の長半径について、GRS80やWGS84では6,378,137mだが、ヒュベニが公式を発表した1950年はBesselを前提としていたので、ここでは6,377,397mを使用する。
定数として計算できるものを代入して簡略化していく。
d = sqrt((M*Δφ)^2+(N*cos(φ)*Δλ)^2)
M = 6334834 / sqrt ((1-0.0066744*sin(φ)^2)^3)
N = 6377397 / sqrt (1-0.0066744*sin(φ)^2)
φ, Δφ, Δλ はラジアンに換算して代入する
表計算ソフトで一発で計算するための式は以下の通り。セルの緯度経度の設定は上記と同じ。単位はm。
= sqrt ((6334834 / sqrt ((1-0.006674*sin((B1+B3)/2*Pi()/180)^2)^3)*(B1-B3)*Pi()/180)^2 +( 6377397 / sqrt (1-0.006674*sin((B1+B3)/2*Pi()/180)^2)*cos((B1+B3)/2*Pi()/180)*(B2-B4)*Pi()/180)^2)
平均緯度は単純に2地点の緯度の算術平均とした。緯度が離れていたり、距離が長い場合には、算術平均では少しまずいのではないかと思うのだが、距離が短かければ、おおよそそれらしい数値が得られる。
上記の例と同様の緯度経度で計算すると、287,309.947mと計算される。真球近似式の数値とは152m程度の差があるが、国土地理院サイトで計算した距離とは16mしか差がない。
真球近似式とヒュベニ近似式を比較
一番最初の例をまとめて比較してみる。
| (N36, E138) –> (E38, E136) | 距離(m) | 誤差(m) |
| 真球近似式 | 287,461.514 | 136.063 |
| ヒュベニ近似式 | 287,309.948 | -15.503 |
| 国土地理院サイト | 287,325.451 | 0.000 |
この例では、ヒュベニ近似式は真球近似式よりも誤差が少なかった。
また、地球の赤道円周は40075kmで、赤道から極までの長さは10001.97kmとされている。
| 実測値 | 真球 | ヒュベニ | |
| 赤道円周 | 40075km | 40030km | 40070km |
| 赤道から極 | 10001.97km | 10007.54km | 10000.75km |
と計算してみると、ヒュベニの式の方が実測値に近いことがわかる。
東京(緯度:35.675899、経度:139.744854)、ロンドン(緯度:51.475831、経度:-0.130997)の例をみると、国土地理院の計算サイトでは測地線長:9,588,734.165(m)となるが、真球計算では9565.134km、ヒュベニでは11432.697kmとヒュベニの誤差が耐え難い大きさになる。
| 国土地理院 | 真球 | ヒュベニ | |
| 東京-ロンドン距離 | 9,588,734m | 9,565,134m | 11,432,697m |
| 国土地理院との差 | 0m | -23,600m | 1,843,963m |
ヒュベニでは始点と終点が、緯線と経線が直角となる三角形の斜辺に近似できる時には有効だということだ。上記の東京=ロンドンのように緯度が上がってまた下がるようなコースをとる場合にはうまく計算できない。
東京-沖縄を測ってみると、国土地理院サイトでは1,553,290.759(m)が、真球で1553.679km、ヒュベニで1555.532kmとなる。距離が1000km以下となる場合に適しているようだ。
地表の距離を求めるのは、実は複雑である。国土地理院サイトにある計算式はあまりに複雑である。途中である値の絶対値が10のマイナス15乗を下回るまで反復して計算せよという部分がある。表計算ソフトの1セルには書けないのだ。
回転楕円体の表面の最短距離を計算するのはこんなにも複雑である。近似値ではない値を求めようとしても単純にはいかない。1000km以内で精度を求めるならばヒュベニ近似式を使いのが良いが、それ以上長い距離を計算するのならば真球近似式がシンプルで計算コストが低い。
前の記事:
緯線に沿った距離、あるいは経線に沿った距離を求めるというのであれば、こちらの記事の計算では回転楕円体として計算しているので精度が高い。


2地点の緯度・経度から、Excelで距離を計算する事が出来ないかと思い、調べていたところ、このページに辿り着きました。表計算ソフトで一発で計算するための式は、数学に疎い私にとって大変有難いものであり、是非活用させて頂こうと思います。
ところで、ヒュベニの近似式でa:回転楕円体の長半径は6,378,137mと記載されているのに、N:卯酉線曲率半径を求める際、aを6,377,397mで計算しているように見えるのですが、 何か理由があるのでしょうか。数学の知識が不足している故、的外れな質問でしたら、申し訳ありません。ご教示いただけますと幸甚に存じます。
田中さん
コメントありがとうございます。
数学的な話ではなく、地球の長半径について、歴史的に数値の変化があったからです。
Bessel楕円体は1841年に定められてから長い間使用され、その後1980年にGRS80、1984年にWGS84が定義されました。日本では2002年までBesselが使われていました。
GRS80やWGS84の長半径は6,378,137mとされていますが、ヒュベニの公式の発表された1950年はBesselですので6,377,397mを計算式では使用しました。
一方、ヒュベニの近似式の項目説明ではa:長半径に対して、つい現在のGRS80やWGS84の数値を記載してしまったのですが、ヒュベニ式でBesselの数値を使うことと矛盾がありました。説明としては不適切でした。
ご指摘ありがとうございました。記事本文については修正して、また複数の長半径についての注釈を追記しようと思います。
どうもありがとうございました。
ご丁寧なご説明を頂いた事に深く感謝いたしております。
ベッセル楕円体の数値を用いて、計算されていること承知いたしました。
また、複数の長半径について、注釈を追記いただけるとの事で、楽しみにしております。
大変勉強になりました。
此の度は誠に有難う御座いました。
D=6371・arccos(cos(lat1)+cos(lat2)∗cos(lon2−lon1)+sin(lat1)∗sin(lat2))
は
D=6371・arccos(cos(lat1)∗cos(lat2)∗cos(lon2−lon1)+sin(lat1)∗sin(lat2))
ではないですか
maya21さん
コメントありがとうございます。
ご指摘の通り、数式の表記がおかしかったので、本日修正しました。
Excel式は合っているので、計算には支障がなかったと思います。
ありがとうございました。
こんにちは。Hubenyの論文自体は「ガウス平均緯度式(近距離近似)」の級数展開形を与えたものです。また(日本で言われるような)一次近似した簡素な式とは無関係です。級数展開しない式を使う方が手っ取り早い(?)かと思いました。下記も参考になりそうです。
https://ja.wikipedia.org/wiki/経緯度#回転楕円体面に沿う最短距離の式
kkddさん
コメントありがとうございます。「ガウスの平均緯度法」の級数展開しない式についても参考にしてみたいと思います。