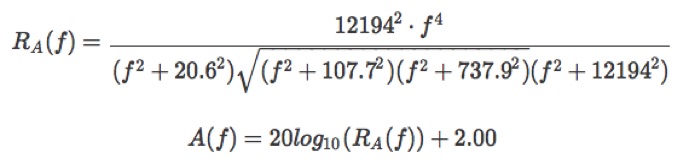音の大きさとは
音の大きさというのは、一体どういうことか?
音量とデシベル、音圧、人の感覚としての音の大きさ、そしてA特性などについて説明する。Excel式も示す。
音波について
そもそも音というのは、空気中であれば空気の振動である。周波数が高ければ高音になり、低ければ低音になる。
空気の振動は、空気が押したり引いたりする震えとなって、周囲に伝わっていく。空気中に密度の高いところ低いところ(疎)ができて伝わっていく波なので、疎密波という。
この密と疎の違いが大きければ大きな音になり、小さければ小さな音になる。この音の圧力を音圧という。音圧が大きければ大きな音だということだ。
音圧と音圧レベル
音圧は、大気を押す力で、大気圧からの変動分であり、単位はパスカル(Pa)である。
音圧をパスカル(Pa)を使って表現できるのだが、人にとって日常的な音をパスカルで表現しようとすると、数値の大小が非常に大きく使いにくいため、通常はデシベル(dB)で表現したものを使用する。これは音圧レベルという。
かつて、人間の最小可聴音圧は1KHzの音では20µPaとされていた経緯があり、音圧レベルは、20µPaを基準音圧として、デシベルを使って比率で表すこととなった。
音圧はパスカルで実際の値、音圧レベルは20µPaを基準音圧とした比率表現なのである。
デシベル(dB)とは?
20µPaを基準音圧とした比率によって音の大きさを表現しようとしたのが、音圧のデシベルである。
騒音計、オーディオ・アンプの出力メーター、録音機器など、無線機などに付いていることが多い。
デシベルというのは、音圧や電圧・電力などで使うことが多い。本来、デシベルは絶対値を表現したものではなく、相対量を示すためのものであった。
今では、音圧レベルのように基準値を定めて絶対量として表現することもある。デシベルといっても、デシベルって、よく分からないというのは、これらの機器の単位がそれぞれ異なっており、電圧であったり音圧であったりするからだろう。
音圧レベルとしてのデシベル
音圧レベルの計算
音圧レベルとLとして、基準音圧をPsとし、対象となる音圧をPtとすると次の式に表現できる。[音圧レベルの公式]
$$L = 20 \log_{10} \left( \frac{P_{t}}{P_{s}} \right) dB$$
デシベル(dB)は対数表現で、音圧の場合は20dBで音圧は10倍になる。10dBでは約3.2倍、6dBで約2倍、3dBでは約1.4倍となる。
20dBでは10倍で、40dBでは100倍、60dBでは1000倍で、20dB増える毎に10倍になる。
すなわち、0dBでは音圧20µPaを示し、20dBでは200µPa、40dBでは2000µPa、60dBでは20000µPa、80dBでは200000µPa、100dBでは2000000µPa(=2Pa)を示す。
表にして示すと以下の通り。
[音圧レベル(dB)と相対量]
| デシベル(dB) | 相対量 |
| -3 | 0.7079 |
| -2 | 0.7943 |
| -1 | 0.8913 |
| 0 | 1.0000 |
| 1 | 1.1220 |
| 2 | 1.2589 |
| 3 | 1.4125 |
| 4 | 1.5849 |
| 5 | 1.7783 |
| 6 | 1.9953 |
| 7 | 2.2387 |
| 8 | 2.5119 |
| 9 | 2.8184 |
| 10 | 3.1623 |
| 11 | 3.5481 |
| 12 | 3.9811 |
| 13 | 4.4668 |
| 14 | 5.0119 |
| 15 | 5.6234 |
| 16 | 6.3096 |
| 17 | 7.0795 |
| 18 | 7.9433 |
| 19 | 8.9125 |
| 20 | 10.0000 |
| 21 | 11.2202 |
| 22 | 12.5893 |
| 23 | 14.1254 |
| 24 | 15.8489 |
| 25 | 17.7828 |
| 26 | 19.9526 |
| 27 | 22.3872 |
| 28 | 25.1189 |
| 29 | 28.1838 |
| 30 | 31.6228 |
| 31 | 35.4813 |
| 32 | 39.8107 |
| 33 | 44.6684 |
| 34 | 50.1187 |
| 35 | 56.2341 |
| 36 | 63.0957 |
| 37 | 70.7946 |
| 38 | 79.4328 |
| 39 | 89.1251 |
| 40 | 100.0000 |
| 41 | 112.2018 |
| 42 | 125.8925 |
| 43 | 141.2538 |
| 44 | 158.4893 |
| 45 | 177.8279 |
| 46 | 199.5262 |
| 47 | 223.8721 |
| 48 | 251.1886 |
| 49 | 281.8383 |
| 50 | 316.2278 |
| 51 | 354.8134 |
| 52 | 398.1072 |
| 53 | 446.6836 |
| 54 | 501.1872 |
| 55 | 562.3413 |
| 56 | 630.9573 |
| 57 | 707.9458 |
| 58 | 794.3282 |
| 59 | 891.2509 |
| 60 | 1 000.0000 |
| 61 | 1 122.0185 |
| 62 | 1 258.9254 |
| 63 | 1 412.5375 |
| 64 | 1 584.8932 |
| 65 | 1 778.2794 |
| 66 | 1 995.2623 |
| 67 | 2 238.7211 |
| 68 | 2 511.8864 |
| 69 | 2 818.3829 |
| 70 | 3 162.2777 |
| 71 | 3 548.1339 |
| 72 | 3 981.0717 |
| 73 | 4 466.8359 |
| 74 | 5 011.8723 |
| 75 | 5 623.4133 |
| 76 | 6 309.5734 |
| 77 | 7 079.4578 |
| 78 | 7 943.2823 |
| 79 | 8 912.5094 |
| 80 | 10 000.0000 |
| 81 | 11 220.1845 |
| 82 | 12 589.2541 |
| 83 | 14 125.3754 |
| 84 | 15 848.9319 |
| 85 | 17 782.7941 |
| 86 | 19 952.6231 |
| 87 | 22 387.2114 |
| 88 | 25 118.8643 |
| 89 | 28 183.8293 |
| 90 | 31 622.7766 |
| 91 | 35 481.3389 |
| 92 | 39 810.7171 |
| 93 | 44 668.3592 |
| 94 | 50 118.7234 |
| 95 | 56 234.1325 |
| 96 | 63 095.7344 |
| 97 | 70 794.5784 |
| 98 | 79 432.8235 |
| 99 | 89 125.0938 |
| 100 | 100 000.0000 |
| 110 | 316 227.7660 |
| 120 | 1 000 000.0000 |
| 130 | 3 162 277.6602 |
音の大きさの目安
ここで一般的な音の大きさの目安を示す。あくまで参考例であるので、「騒々しい事務所」など苦しいものもあるが、ある程度一般的な具体例をまとめた。おおよその目安として欲しい。
[音の大きさの目安]
| 一般的な目安 | dB | 参考例 |
| 聴力機能に障害 | 120 | 飛行機のエンジンの近く、落雷(1km) |
| 110 | 自動車のクラクション(2m) | |
| きわめてうるさい | 100 | ライブハウス、電車が通るガード下 |
| 90 | 犬の鳴き声(2m)、カラオケ店内 | |
| うるさい | 80 | 走行中の地下鉄車内、救急車サイレン(2m) |
| 70 | 騒々しい事務所、セミの鳴き声(2m) | |
| 普通 | 60 | 走行中の自動車内、普通の会話 |
| 50 | 静かな事務所、小さい声 | |
| 静か | 40 | 図書館内、昼の静かな住宅地 |
| 30 | 深夜の郊外 | |
| きわめて静か | 20 | 雪の降る音、無音室 |
音圧レベルのデシベルのExcel計算式
ExcelでA1のセルに元の数値を入れる場合のExcel計算式を示す。相対量というのはここでは「音圧の観測値(µPa) / 音圧の基準値(=20µPa)」をいう。
デシベル(dB)を相対量に変換するのは次の通り。
=10^(A1/20)
セル[A1]に 3 と入力すれば、1.41253…と計算されるはずだ。
相対量をデシベル(dB)に変換するのは次の通り。
=20*LOG10(A1)
セル[A1]に2と入力すれば、6.02060…。
距離による音量への影響
音の大きさは、音源からの距離によっても変わる。遠くなれば音は小さくなる。
全周囲に球面用に広がって行く音は、点音源という。他にも、複数の車両が連結された電車の音などは円筒状にひろがるので、線音源と呼ぶ。また、大きな建物の壁が一様に振動して発生した音はある程度の距離までは平行移動するように伝わり、これを面音源という。
点音源の場合、音の強さは距離の二乗に反比例する。もちろん実際には、周囲の壁の反響や、音源の指向性などによっても影響を受ける。
距離1mと距離2mの音の強さの関係は、12 : 22 = 1 : 4 となる。
Excelでは、=10*LOG10(1/2^2) と計算式を入れ、-6.020599… と計算できる。
=10*LOG10(1/A1^2) として、A1に測りたい距離を入れれば、距離1mに比した音量の違いを計算できる。
[距離・減衰比(dB)の関係]
| 距離(m) | 減衰比(dB) |
| 1 | 0.00 |
| 2 | -6.02 |
| 3 | -9.54 |
| 4 | -12.04 |
| 5 | -13.98 |
| 6 | -15.56 |
| 7 | -16.90 |
| 8 | -18.06 |
| 9 | -19.08 |
| 10 | -20.00 |
| 20 | -26.02 |
| 30 | -29.54 |
| 40 | -32.04 |
| 50 | -33.98 |
1mの距離で90dBの音は、30m離れたとすると約60dBで聞こえるということだ。
複数の音圧レベルの和
複数の音が重なる場合に、音量はどのように変化するのか。
60dBの音を出す機械と70dBの音を出す機械が両方動いた時には、どうなるか。[複数の音圧レベルの和]
60dBとは、=10^(60/10) =1,000,000 倍ということで、
70dBは、=10^(70/10) = 10,000,000 倍なので、
これを足し合わせると、11,000,000 となる。
=10 * Log10 ( 11000000) と計算すると、70.4139… と計算されるので、約70.4dBとなる。
70dBの音が二つ鳴ると、音量は =10^(70/10) * 2 = 20,000,000 なので、
=10 * Log10(20000000) と入力して、73.0102… と計算される。73dBである。
同じ音圧レベルの音が複数同時に鳴る場合には、次のように増加する。
[音の数と音圧レベルの増加量]
| 音の数 | 音圧レベルの増加量(dB) |
| 1 | 0.00 |
| 2 | 3.01 |
| 3 | 4.77 |
| 4 | 6.02 |
| 5 | 6.99 |
| 6 | 7.78 |
| 7 | 8.45 |
| 8 | 9.03 |
| 9 | 9.54 |
| 10 | 10.00 |
人間にとっての音量
音圧の大小で音量が決まる。物理的には、定められた基準で音圧を機械で測定すれば音量を測れる。
それでは音圧を測定すれば、人にとって大きい音か小さい音か決まるのかというと、実はそう簡単ではない。
周波数による感覚の違い
光が波長(周波数)によって、見えやすい色と見えにくい色、見えない色に分かれるように、音も周波数によって、よく聞こえる音とよく聞こえない音がある。
モスキートトーンという言葉をご存知かもしれない。10000Hzを超える高い音は歳をとるほど聞こえにくくなってくる。コントラバスなどの低い音も、音圧に比して音の大きさを感じにくい。
つまり、高音と低音は音が小さく聞こえるということで、中音域では低い音圧でも大きな音に聞こえるのである。最近あまり聞くことがないけれども、時報の音は440Hzの音が3つ鳴ってから、880Hzの音が正時を叩く。
この880Hzという周波数は、人にとって大変敏感に感じ取ることのできる音域なのである。
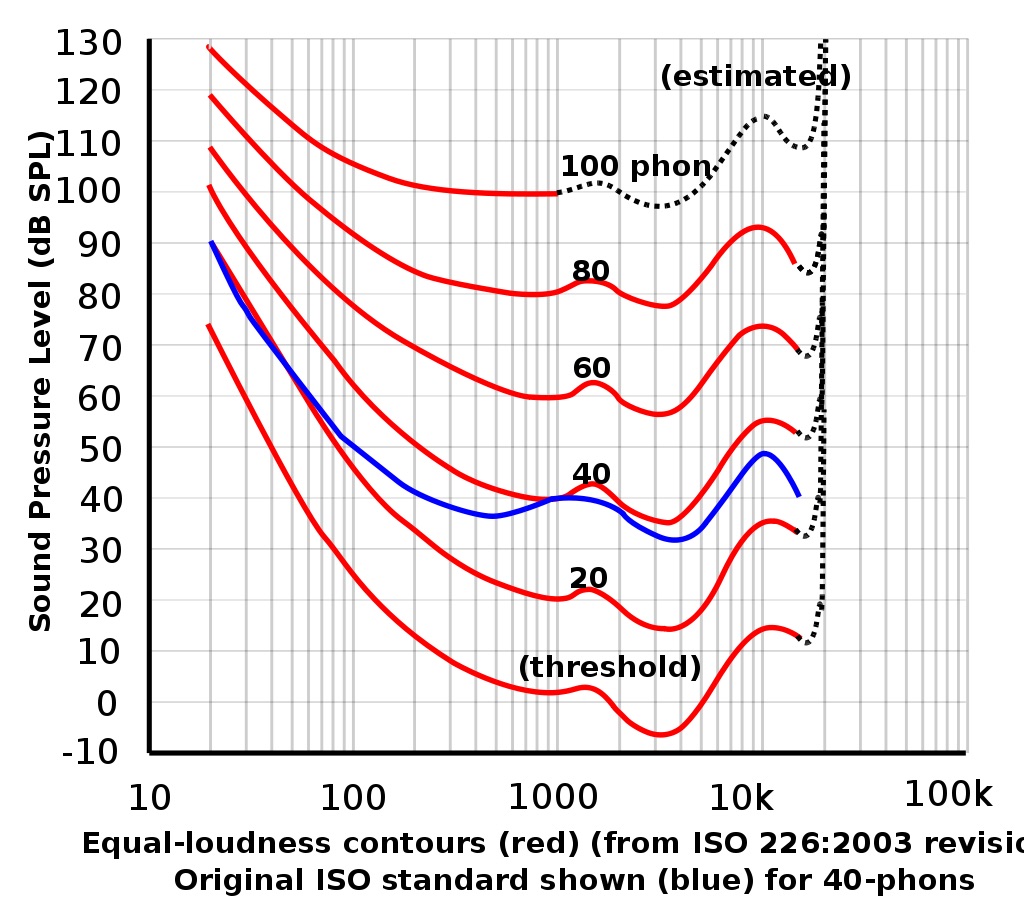
人間の耳には周波数による感受性というのがあって、周波数によって耳の反応が異なる。下のグラフで、下がっているところが音が大きく聞こえるところである。1000Hzあたりにひとつ、1000Hzと10KHzの間にもう一つピークがある。
ラウドネス曲線
次のグラフは、ラウドネス曲線という。ラウドネスというのは、人が耳で聞いたときに感じる音の大きさのことである。1000Hzの純音で20dBの音量を基準にして、周波数を上げ下げして、音量が一定に聞こえるように出力(dB)を調整したものが赤い線となっている。同様に、他の音量についても赤い線でグラフになっている。
ラウドネス曲線は、年齢、人種、環境など多くの要因によって差があり、一様ではない。この曲線が示しているのは、ラウドネスレベルという。
[ラウドネス曲線]
ラウドネスとラウドネスレベルの関係
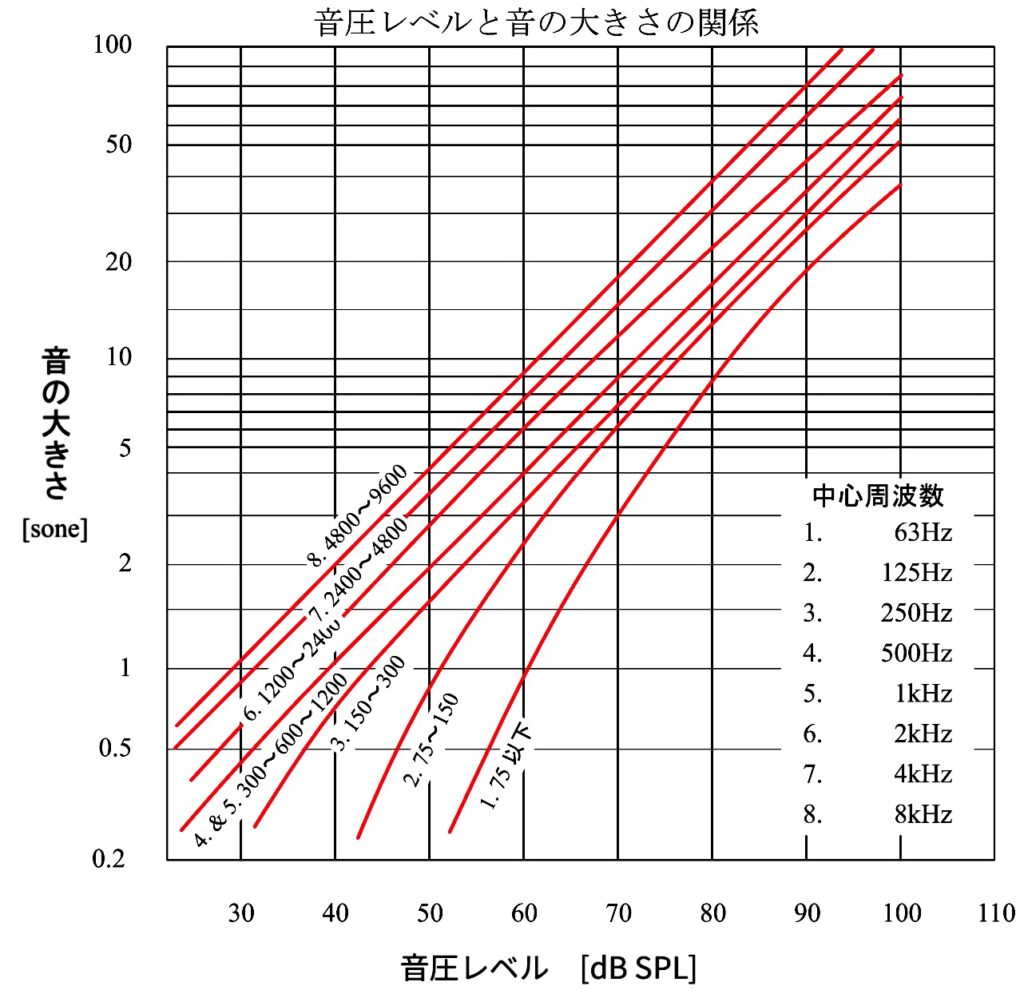
ラウドネスというのは、人間の聴覚が感じる音の大小を示す心理量のことで、ラウドネスの単位は、ソーン(sone)という。周波数1kHz・音圧レベル40dBの純音を聞いたときの音の大きさを1 sone と定義する。
心理量であるので、人それぞれで単純な計測はできないが、統計的に処理された研究をベースに、ラウドネスはISO532で規格化されている。これがラウドネス曲線である。ラウドネス曲線が示しているのがラウドネスレベルである。
ラウドネスレベルの単位はphonである。phonは、周波数1kHzの50dBを50phon、60dBを60phonのように、dBとphonを関係づける。
そして、周波数1kHz・音圧レベル40dBのただ1点のみで、ソーン(sone)とphonが完全に一致する。そもそものソーンの定義となっているためである。
1kHzの時に、1soneは40dBであるが、2soneの時にはほぼ50dB、60dBではほぼ8soneとなっている。特定の範囲内で、おおむね近似するものとして扱われている。
[ラウドネスとラウドネスレベルの関係]
| sone(ソーン) | phon(フォン) |
| 0.5 | 30 |
| 1 | 40 |
| 2 | 50 |
| 4 | 60 |
| 8 | 70 |
| 16 | 80 |
| 32 | 90 |
[音圧レベルと音の大きさの関係図]
音のA特性とは?
A特性の考え方
A特性とは、先ほどのラウドネスカーブをベースにして、計算しやすいよう単純化されている。騒音計などに組み込みやすいように考え出されたものである。とはいえ、決して単純な式ではない。
この式は、音圧からラウドネスに正確に変換できるものではない。近似式であるけれども、ラウドネス曲線にぴったり近似しているというわけではない。ゆるやかな近似である。
[周波数とA特性補正値の関係図]
この式の目的は、物理的な音圧が人間にとってどれだけの音量か、換算する式である。このA特性は、IECで規格化されているので、音響や騒音に関係する業界で広く利用されており、音量計、騒音計などに組み込まれていることが多い。
ただし、この式は実用的ではないので、簡単にExcelで計算できるようにした。特定の周波数の音圧が、A特性では、どれだけ音圧を補正値としてプラスするかというExcel計算式を次に示す。
A特性補正値をExcelで計算
インプットは、周波数で単位はHz、アウトプットはA特性補正値で単位はdB だ。単位は[ ]、次の f や A{f) は上の式に対応する項目。
周波数[Hz] f
A特性補正値[dB] A(f)
f をセルA1に設定すると、A特性補正値のExcel計算式は・・・
=20 * LOG(( ( (12194^2)*(A1^4) ) / ( (A1^2+20.6^2) * ( (A1^2+107.7^2) * (A1^2 + 737.9^2) ) ^0.5 * (A1^2+12194^2) ) )) + 2
これで、fに 20 と入力すると、補正値は -50.4 と計算される。
例)
周波数1000Hzの補正値を0、周波数が50Hzの補正値を-30とすると、1000Hzで補正前の50dBの音と、50Hzで同じく補正前の80dBの音が、ほぼ同じ音量の評価値になるということだ。
計算結果を表にする。
[周波数とA特性補正値の表]
| 周波数(Hz) | A特性補正値 |
| 20.0 | -50.3947 |
| 25.0 | -44.8205 |
| 31.5 | -39.5289 |
| 40.0 | -34.5392 |
| 50.0 | -30.2750 |
| 63.0 | -26.2228 |
| 80.0 | -22.3977 |
| 100.0 | -19.1450 |
| 125.0 | -16.1897 |
| 160.0 | -13.2443 |
| 200.0 | -10.8471 |
| 250.0 | -8.6748 |
| 315.0 | -6.6438 |
| 400.0 | -4.7739 |
| 500.0 | -3.2478 |
| 630.0 | -1.9085 |
| 800.0 | -0.7946 |
| 1000.0 | 0.0001 |
| 1250.0 | 0.5763 |
| 1600.0 | 0.9931 |
| 2000.0 | 1.2017 |
| 2500.0 | 1.2710 |
| 3150.0 | 1.2014 |
| 4000.0 | 0.9636 |
| 5000.0 | 0.5544 |
| 6300.0 | -0.1156 |
| 8000.0 | -1.1469 |
| 10000.0 | -2.4916 |
単音であれば、その音に対する周波数から、A特性補正値を計算して、その数値を元の音圧レベルに加算すれば、A特性の数値を得られる。
実際には、音は単音だけでなっていることは少なく、複雑に多くの周波数が入り混じっており、音の強弱の変化もあり、音の長さ、音色(倍音の影響)によっても感覚は異なる。一口に音量といっても、実際には非常に複雑である。
用語集
| 用語 | 説明 |
| 音量 | 音の大きさ・強さの度合い。ボリューム。 |
| 音圧 | 物理量、単位はパスカル、Pa。空気中における、大気圧との差。パスカル、Paでは通知を取り扱いにくいため、通常は音圧レベルを用いる。音圧レベルの単位は、dBを使う。 |
| 音圧レベル | 音圧を特定の基準値からの相対量として表現したもの。単位は、dB、デシベル。20μPa を 0 dB と定める。 例)200μPa = 20dB、2000μPa = 40dB、20000μPa = 60dB、200000μPa = 80dB、2000000μPa = 2 Pa = 100dB 。dB SPL と表記されることもある。 |
| デシベル | 対数を使った相対量の表現で、電圧、音圧、電力などに用いる。電力では 10dB が10倍、電圧や音圧では20dB が10倍となる。 (比率を底10の対数で表したものに10をかけたもの。電圧や音圧では比率に2乗するため、2乗を外して20をかけた数値となる。) |
| ラウドネス | 人間の聴覚が感じる音の大小を示す心理量。ラウドネスの単位は、ソーン(sone)。周波数1kHz・音圧レベル40dBの純音を聞いたときの音の大きさを1 sone と定義。ラウドネスは、ISO532で規格化されている。 |
| ソーン、sone | ラウドネスの単位。人間の聴覚が感じる音の大小を示す単位。周波数1kHz・音圧レベル40dBの純音を聞いたときの音の大きさを1 sone と定義。1 sone の2倍の大きさの音を 2 sone、2 sone の2倍の大きさは 4 sone 。周波数が1kHz以外の音に対しては、等ラウドネス曲線を使用して補正される。 |
| ラウドネスレベル | 等ラウドネス曲線を使用して、周波数と音圧レベルと心理量との関係を客観的な値として取り扱えるようにしたもの。周波数1kHzの純音のdB値がフォンに等しい。1KHzで40dBの純音は 40 phonである。同様に、1kHz・60dBの純音は60 phonである。他の周波数の純音に対しては、ISO 226:2003で規格化された等ラウドネス曲線を使用する。 |
| Phon、 フォン |
ラウドネスレベルの単位。周波数1kHzの純音のdB値はフォン(phon)と等しい。1KHzで40dBの純音は 40 phonである。また、1 sone は1kHz・40dBの純音と定義されているので、1kHz・純音・音圧レベル 40 dB = 40 phon = 1 sone である。 |
| ホン | 日本で使われていた騒音レベルの単位。A特性はホン(A)のように表記された。現在ではdBを使う。また、Phon(フォン)と同じ意味で、ホン、ホーンという人もおり紛らわしい。 |
| 騒音レベル | 音圧レベルに対して、A特性、C特性、などで補正することで、一般化したもの。A特性は、IEC 61672:2003で規格化された補正方法で、広く使われている。A特性による騒音レベルを、dB(A)、dBAと表記されていることもある(この表記はISOやJISでは推奨されない)。 |
| ラウドネスとラウドネスレベルの関係 | 定義により、周波数1kHz・純音・音圧レベル 40 dB = 1 sone である。40 dBから10 dB 上がるごとに、sone は2倍になるという。 40 dB = 1 sone、50 dB = 2 sone、60 dB = 4 sone、70 dB = 8 sone、80 dB = 16 sone、90 dB = 32 sone。ということは、人間の聴覚にとって、40 phon から 10 phon 上がるごとに、2倍になるということになる。 (図「音圧レベルと音の大きさの関係」参照) |
| 等ラウドネス曲線 | 純音に対して音の大きさが等しいと感じる組み合わせを、周波数と音圧の図に等高線として示したもの。周波数1kHzで音圧20dBの音を20 phon、同じく30dBの音を 30 phon、・・・90 phon 位まで線がある。 研究者によって、さまざまな等ラウドネス曲線が作成された。ISO 226で定義された国際規格の標準等ラウドネス曲線が広く使われている。正式規格名称は、ISO 226:2003 Acoustics – Normal equal-loudness-level contours 。 |